Derivation: Maximum Likelihood for Boltzmann Machines

In this post I will review the gradient descent algorithm that is commonly used to train the general class of models known as Boltzmann machines. Though the primary goal of the post is to supplement another post on restricted Boltzmann machines, I hope that those readers who are curious about how Boltzmann machines are trained, but have found it difficult to track down a complete or straight-forward derivation of the maximum likelihood learning algorithm for these models (as I have), will also find the post informative.

First, a little background: Boltzmann machines are stochastic neural networks that can be thought of as the probabilistic extension of the Hopfield network. The goal of the Boltzmann machine is to model a set of observed data in terms of a set of visible random variables  and a set of latent/unobserved random variables . Due to the relationship between Boltzmann machines and neural networks, the random variables are often are often referred to as “units.” The role of the visible units is to approximate the true distribution of the data, while the role of the latent variables it to extend the expressiveness of the model by capturing underlying features in the observed data. The latent variables are often referred to as hidden units, as they do not result directly from the observed data and are generally marginalized over to obtain the likelihood of the observed data,  i.e.

,

 

where is the joint probability distribution over the visible and hidden units based on the current model parameters . The general Boltzmann machine defines through a set of weighted,  symmetric connections between all visible and hidden units (but no connections from any unit to itself). The graphical model for the general Boltzmann machine is shown in Figure 1.

Figure 1: Graphical Model of the Boltzmann machine (biases not depicted).

Given the current state of the visible and hidden units, the overall configuration of the model network is described by a connectivity function , parameterized by :

The parameter matrix defines the connection strength between the visible and hidden units. The parameters and define the connection strength amongst hidden units and visible units, respectively. The model also includes a set of  biases and that capture offsets for each of the hidden and visible units.

The Boltzmann machine has been used for years in field of statistical mechanics to model physical systems based on the principle of energy minimization. In the statistical mechanics, the connectivity function is often referred to the “energy function,” a term that is has also been standardized in the statistical learning literature. Note that the energy function returns a single scalar value for any configuration of the network parameters and random variable states.

Given the energy function, the Boltzmann machine models the joint probability of the visible and hidden unit states as a Boltzmann distribution:

The partition function is a normalizing constant that is calculated by summing over all possible states of the network . Here we assume that all random variables take on discrete values, but the analogous derivation holds for continuous or mixed variable types by replacing the sums with integrals accordingly.

The common way to train the Boltzmann machine is to determine the parameters that maximize the likelihood of the observed data. To determine the parameters, we perform gradient descent on the log of the likelihood function (In order to simplify the notation in the remainder of the derivation, we do not include the explicit dependency on the parameters . To further simplify things, let’s also assume that we calculate the gradient of the likelihood based on a single observation.):

The gradient calculation is as follows:

Here we can simplify the expression somewhat by noting that , that , and also that is a constant:

If we also note that , and use the definition of conditional probability , we can further simplify the expression for the gradient:

Here is the expected value under the distribution . Thus the gradient of the likelihood function is composed of two parts. The first part is expected gradient of the energy function with respect to the conditional distribution . The second part is expected gradient of the energy function with respect to the joint distribution over all variable states. However, calculating these expectations is generally infeasible for any realistically-sized model, as it involves summing over a huge number of possible states/configurations. The general approach for solving this problem is to use Markov Chain Monte Carlo (MCMC) to approximate these sums:

Here is the sample average of samples drawn according to the process . The first term is calculated by taking the average value of the energy function gradient when the visible and hidden units are being driven by observed data samples. In practice, this first term is generally straightforward to calculate. Calculating the second term is generally more complicated and involves running a set of Markov chains until they reach the current model’s equilibrium distribution (i.e. via Gibbs sampling, Metropolis-Hastings, or the like), then taking the average energy function gradient based on those samples. See this post on MCMC methods for details. It turns out that there is a subclass of Boltzmann machines that, due to a restricted connectivity/energy function (specifically, the parameters ), allow for efficient MCMC by way of blocked Gibbs sampling. These models, known as restricted Boltzman machines have become an important component for unsupervised pretraining in the field of deep learning and will be the focus of a related post.

MCMC: The Gibbs Sampler

In the previous post, we compared using block-wise and component-wise implementations of the Metropolis-Hastings algorithm for sampling from a multivariate probability distribution. Component-wise updates for MCMC algorithms are generally more efficient for multivariate problems than blockwise updates in that we are more likely to accept a proposed sample by drawing each component/dimension independently of the others. However, samples may still be rejected, leading to excess computation that is never used. The Gibbs sampler, another popular MCMC sampling technique, provides a means of avoiding such wasted computation. Like the component-wise implementation of the Metropolis-Hastings algorithm, the Gibbs sampler also uses component-wise updates. However, unlike in the Metropolis-Hastings algorithm, all proposed samples are accepted, so there is no wasted computation.

The Gibbs sampler is applicable for certain classes of problems, based on two main criterion. Given a target distribution , where , ),  The first criterion is 1) that it is necessary that we have an analytic (mathematical) expression for the conditional distribution of each variable in the joint distribution given all other variables in the joint. Formally, if the target distribution is -dimensional, we must have individual expressions for

.

Each of these expressions defines the probability of the -th dimension given that we have values for all other () dimensions. Having the conditional distribution for each variable means that we don’t need a proposal distribution or an accept/reject criterion, like in the Metropolis-Hastings algorithm. Therefore, we can simply sample from each conditional while keeping all other variables held fixed. This leads to the second criterion 2) that we must be able to sample from each conditional distribution. This caveat is obvious if we want an implementable algorithm.

The Gibbs sampler works in much the same way as the component-wise Metropolis-Hastings algorithms except that instead drawing from a proposal distribution for each dimension, then accepting or rejecting the proposed sample, we simply draw a value for that dimension according to the variable’s corresponding conditional distribution. We also accept all values that are drawn. Similar to the component-wise Metropolis-Hastings algorithm, we step through each variable sequentially, sampling it while keeping all other variables fixed. The Gibbs sampling procedure is outlined below

1. set
2. generate an initial state
3. repeat until

set

for each dimension

draw from

To get a better understanding of the Gibbs sampler at work, let’s implement the Gibbs sampler to solve the same multivariate sampling problem addressed in the previous post.

Example: Sampling from a bivariate a Normal distribution

This example parallels the examples in the previous post where we sampled from a 2-D Normal distribution using block-wise and component-wise Metropolis-Hastings algorithms. Here, we show how to implement a Gibbs sampler to draw samples from the same target distribution. As a reminder, the target distribution is a Normal form with following parameterization:

with mean

and covariance

In order to sample from this distribution using a Gibbs sampler, we need to have in hand the conditional distributions for variables/dimensions and :

(i.e. the conditional for the first dimension, )

and

(the conditional for the second dimension, )

Where is the previous state of the second dimension, and is the state of the first dimension after drawing from . The reason for the discrepancy between updating and using states and , can be is seen in step 3 of the algorithm outlined in the previous section. At iteration we first sample a new state for variable conditioned on the most recent state of variable , which is from iteration . We then sample a new state for the variable conditioned on the most recent state of variable , which is now from the current iteration, .

After some math (which which I will skip for some brevity, but see the following for some details), we find that the two conditional distributions for the target Normal distribution are:

and

,

which are both univariate Normal distributions, each with a mean that is dependent on the value of the most recent state of the conditioning variable, and a variance that is dependent on the target covariances between the two variables.

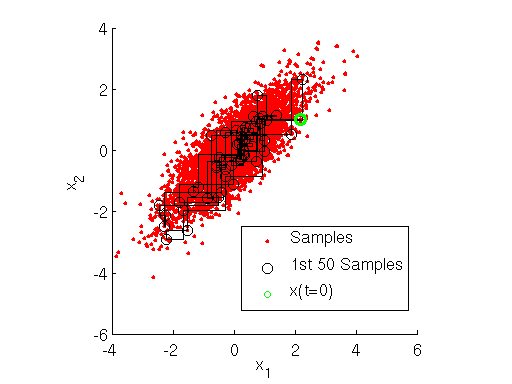
Using the above expressions for the conditional probabilities of variables and , we implement the Gibbs sampler using MATLAB below. The output of the sampler is shown here:

Gibbs sampler Markov chain and samples for bivariate Normal target distribution

Inspecting the figure above, note how at each iteration the Markov chain for the Gibbs sampler first takes a step only along the direction, then only along the direction.  This shows how the Gibbs sampler sequentially samples the value of each variable separately, in a component-wise fashion.

% EXAMPLE: GIBBS SAMPLER FOR BIVARIATE NORMAL
rand('seed' ,12345);
nSamples = 5000;

mu = [0 0]; % TARGET MEAN
rho(1) = 0.8; % rho_21
rho(2) = 0.8; % rho_12

% INITIALIZE THE GIBBS SAMPLER
propSigma = 1; % PROPOSAL VARIANCE
minn = [-3 -3];
maxx = [3 3];

% INITIALIZE SAMPLES
x = zeros(nSamples,2);
x(1,1) = unifrnd(minn(1), maxx(1));
x(1,2) = unifrnd(minn(2), maxx(2));

dims = 1:2; % INDEX INTO EACH DIMENSION

% RUN GIBBS SAMPLER
t = 1;
while t < nSamples
    t = t + 1;
    T = [t-1,t];
    for iD = 1:2 % LOOP OVER DIMENSIONS
        % UPDATE SAMPLES
        nIx = dims~=iD; % *NOT* THE CURRENT DIMENSION
        % CONDITIONAL MEAN
        muCond = mu(iD) + rho(iD)*(x(T(iD),nIx)-mu(nIx));
        % CONDITIONAL VARIANCE
        varCond = sqrt(1-rho(iD)^2);
        % DRAW FROM CONDITIONAL
        x(t,iD) = normrnd(muCond,varCond);
    end
end

% DISPLAY SAMPLING DYNAMICS
figure;
h1 = scatter(x(:,1),x(:,2),'r.');

% CONDITIONAL STEPS/SAMPLES
hold on;
for t = 1:50
    plot([x(t,1),x(t+1,1)],[x(t,2),x(t,2)],'k-');
    plot([x(t+1,1),x(t+1,1)],[x(t,2),x(t+1,2)],'k-');
    h2 = plot(x(t+1,1),x(t+1,2),'ko');
end

h3 = scatter(x(1,1),x(1,2),'go','Linewidth',3);
legend([h1,h2,h3],{'Samples','1st 50 Samples','x(t=0)'},'Location','Northwest')
hold off;
xlabel('x_1');
ylabel('x_2');
axis square

Wrapping Up

The Gibbs sampler is a popular MCMC method for sampling from complex, multivariate probability distributions. However, the Gibbs sampler cannot be used for general sampling problems. For many target distributions, it may difficult or impossible to obtain a closed-form expression for all the needed conditional distributions. In other scenarios, analytic expressions may exist for all conditionals but it may be difficult to sample from any or all of the conditional distributions (in these scenarios it is common to use univariate sampling methods such as rejection sampling and (surprise!) Metropolis-type MCMC techniques to approximate samples from each conditional). Gibbs samplers are very popular for Bayesian methods where models are often devised in such a way that conditional expressions for all model variables are easily obtained and take well-known forms that can be sampled from efficiently.

Gibbs sampling, like many MCMC techniques suffer from what is often called “slow mixing.” Slow mixing occurs when the underlying Markov chain takes a long time to sufficiently explore the values of in order to give a good characterization of . Slow mixing is due to a number of factors including the “random walk” nature of the Markov chain, as well as the tendency of the Markov chain to get “stuck,” only sampling a single region of having high-probability under . Such behaviors are bad for sampling distributions with multiple modes or heavy tails. More advanced techniques, such as Hybrid Monte Carlo have been developed to incorporate additional dynamics that increase the efficiency of the Markov chain path. We will discuss Hybrid Monte Carlo in a future post.

A Brief Introduction to Markov Chains

Markov chains are an essential component of Markov chain Monte Carlo (MCMC) techniques. Under MCMC, the Markov chain is used to sample from some target distribution. To get a better understanding of what a Markov chain is, and further, how it can be used to sample form a distribution, this post introduces and applies a few basic concepts.

A Markov chain is a stochastic process that operates sequentially (e.g. temporally), transitioning from one state to another within an allowed set of states.^†

A Markov chain is defined by three elements:

1. A state space , which is a set of values that the chain is allowed to take
2. A transition operator that defines  the probability of moving from state to  .
3. An initial condition distribution which defines the probability of being in any one of the possible states at the initial iteration .

The Markov chain starts at some initial state, which is sampled from , then transitions from one state to another according to the transition operator .

A Markov chain is called memoryless if the next state only depends on the current state and not on any of the states previous to the current:

(This memoryless property is formally know as the Markov property).

If the transition operator for a Markov chain does not change across transitions, the Markov chain is called time homogenous.  A nice  property of time homogenous Markov chains is that as the chain runs for a long time and , the chain will reach an equilibrium that is called the chain’s stationary distribution:

We’ll see later how the stationary distribution of a Markov chain is important for sampling from probability distributions, a technique that is at the heart of Markov Chain Monte Carlo (MCMC) methods.

Finite state-space (time homogenous) Markov chain

If the state space of a Markov chain takes on a finite number of distinct values, and it is time homogenous, then the transition operator can be defined by a matrix , where the entries of are:

This means that if the chain is currently in the -th state, the transition operator assigns the probability of moving to the  -th state by the entries of -th row of (i.e.  each row of defines a conditional probability distribution on the state space). Let’s take a look at a finite state-space Markov chain in action with a simple example.

Example: Predicting the weather with a finite state-space Markov chain

In Berkeley, CA, there are (literally) only 3 types of weather: sunny, foggy, or rainy (this is analogous to a state-space that takes on three discrete values). The weather patterns are very stable there, so a Berkeley weatherman can easily predict the weather next week based on the weather today with the following transition rules:

If it is sunny today, then

• it is highly likely that it will be sunny next week
  • ,
• it is very unlikely that it will be raining next week
  • 
• and somewhat likely that it will foggy next week
  • 

If it is foggy today then

• it is somewhat likely that it will be sunny next week
  • 
• but slightly less likely that it will be foggy next week
  • ,
• and fairly unlikely that it will be raining next week.
  • ,

If it is rainy today then

• it is unlikely that it will be sunny next week
  • ,
• it is somewhat likely that it will be foggy next week
  • ,
• and it is fairly likely that it will be rainy next week
  • ,

All of these transition rules can be instantiated in a single 3 x 3 transition operator matrix:

Where each row of corresponds to the weather at iteration (today), and each column corresponds to the weather the next week. Let’s say that it is rainy today, what is the probability it will be sunny next week, in two weeks, or in 6 months? We can answer these questions by running a Markov chain from the initial state of “rainy,” transitioning according to . The following chunk of MATLAB code runs the Markov chain.

% FINITE STATE-SPACE MARKOV CHAIN EXAMPLE

% TRANSITION OPERATOR
%     S  F  R
%     U  O  A
%     N  G  I
%     N  G  N
%     Y  Y  Y
P = [.8 .15 .05;  % SUNNY
     .4 .5  .1;   % FOGGY
     .1 .3  .6];  % RAINY
nWeeks = 25

% INITIAL STATE IS RAINY
X(1,:) = [0 0 1];

% RUN MARKOV CHAIN
for iB = 2:nWeeks
    X(iB,:) = X(iB-1,:)*P; % TRANSITION
end

% DISPLAY
figure; hold on
h(1) = plot(1:nWeeks,X(:,1),'r','Linewidth',2);
h(2) = plot(1:nWeeks,X(:,2),'k','Linewidth',2);
h(3) = plot(1:nWeeks,X(:,3),'b','Linewidth',2);
h(4) = plot([15 15],[0 1],'g--','Linewidth',2);
hold off
legend(h, {'Sunny','Foggy','Rainy','Burn In'});
xlabel('Week')
ylabel('p(Weather)')
xlim([1,nWeeks]);
ylim([0 1]);

% PREDICTIONS
fprintf('\np(weather) in 1 week -->'), disp(X(2,:))
fprintf('\np(weather) in 2 weeks -->'), disp(X(3,:))
fprintf('\np(weather) in 6 months -->'), disp(X(25,:))

Finite state-space Markov chain for predicting the weather

Here we see that at week 1 the probability of sunny weather is 0.1. The next week, the probability of sunny weather is 0.26, and in 6 months, there is a 60% chance that it will be sunny. Also note that after approximately 15 weeks the Markov chain has reached the equilibrium/stationary distribution and, chances are, the weather will be sunny. This 15-week period is what is known as the burn in period for the Markov chain, and is the number of transitions it takes the chain to move from the initial conditions to the stationary distribution.

A cool thing about finite state-space time-homogeneous Markov chain is that it is not necessary  to run the chain sequentially through all iterations in order to predict a state in the future. Instead we can predict by first raising the transition operator to the -th power, where is the iteration at which we want to predict, then multiplying the result by the distribution over the initial state, . For instance, to predict the probability of the weather in 2 weeks, knowing that it is rainy today (i.e. ):

and in six months:

These are the same results we get by running the Markov chain sequentially through each number of transitions. Therefore we can calculate an approximation to the stationary distribution from by setting to a large number. It turns out that it is also possible to analytically derive the stationary distribution from (hint: think about the properties of eigenvectors).

Continuous state-space Markov chains

A Markov chain can also have a continuous state space that exists in the real numbers . In this case the transition operator cannot be instantiated simply as a matrix, but is instead some continuous function on the real numbers. Note that the continuous state-space Markov chain also has a burn in period and a stationary distribution. However, the stationary distribution will also be over a continuous set of variables. To get a better understanding of the workings of a continuous state-space Markov chain, let’s look at a simple example.

Example: Sampling from a continuous distribution using continuous state-space Markov chains

We can use the stationary distribution of a continuous state-space Markov chain in order to sample from a continuous probability distribution: we  run a Markov chain for a sufficient amount of time so that it has reached its stationary distribution, then keep the states that the chain visits as samples from that stationary distribution.

In the following example we define a continuous state-space Markov chain. The transition operator is a Normal distribution with unit variance and a mean that is half the distance between zero and the previous state, and the distribution over initial conditions is a Normal distribution with zero mean and unit variance.

To ensure that the chain has moved sufficiently far from the initial conditions and that we are sampling  from the chain’s stationary distribution,  we will choose to throw away the first 50 burn in states of the chain. We can also run multiple chains simultaneously in order to sample the stationary distribution more densely. Here we choose to run 5 chains simultaneously.

% EXAMPLE OF CONTINUOUS STATE-SPACE MARKOV CHAIN

% INITIALIZE
randn('seed',12345)
nBurnin = 50; % # BURNIN
nChains = 5;  % # MARKOV CHAINS

% DEFINE TRANSITION OPERATOR
P = inline('normrnd(.5*x,1,1,nChains)','x','nChains');
nTransitions = 1000;
x = zeros(nTransitions,nChains);
x(1,:) = randn(1,nChains);

% RUN THE CHAINS
for iT = 2:nTransitions
    x(iT,:) = P(x(iT-1),nChains);
end

% DISPLAY BURNIN
figure
subplot(221); plot(x(1:100,:)); hold on;
minn = min(x(:));
maxx = max(x(:));
l = line([nBurnin nBurnin],[minn maxx],'color','k','Linewidth',2);
ylim([minn maxx])
legend(l,'~Burn-in','Location','SouthEast')
title('First 100 Samples'); hold off

% DISPLAY ENTIRE MARKOV CHAIN
subplot(223); plot(x);hold on;
l = line([nBurnin nBurnin],[minn maxx],'color','k','Linewidth',2);
legend(l,'~Burn-in','Location','SouthEast')
title('Entire Chain');

% DISPLAY SAMPLES FROM STATIONARY DISTRIBUTION
samples = x(nBurnin+1:end,:);
subplot(122);
[counts,bins] = hist(samples(:),100); colormap hot
b = bar(bins,counts);
legend(b,sprintf('Markov Chain\nSamples'));
title(['\mu=',num2str(mean(samples(:))),' \sigma=',num2str(var(samples(:)))])

Sampling from the stationary distribution of a continuous state-space Markov chain

In the upper left panel of the code output we see a close up of the first 100 of the 1000 transitions made by the 5 simultaneous Markov chains; the burn in cutoff is marked by the black line. In the lower left panel we see the entire sequence of transitions for the Markov chains. In the right panel, we can tell from the sampled states that the stationary distribution for this chain is a Normal distribution, with mean equal to zero, and a variance equal to 1.3.

Wrapping Up

In the previous example we were able to deduce the stationary distribution of the Markov chain by looking at the samples generated from the chain after the burn in period. However, in order to use Markov chains to sample from a specific target distribution, we have to design the transition operator such that the resulting chain reaches a stationary distribution that matches the target distribution. This is where MCMC methods like the Metropolis sampler, the Metropolis-Hastings sampler, and the Gibbs sampler come to rescue. We will discuss each of these Markov-chain-based sampling methods separately in later posts.

Rejection Sampling

Suppose that we want to sample from a distribution that is difficult or impossible to sample from directly, but instead have a simpler distribution from which sampling is easy.  The idea behind Rejection sampling (aka Acceptance-rejection sampling) is to sample from and apply some rejection/acceptance criterion such that the samples that are accepted are distributed according to .

Envelope distribution and rejection criterion

In order to be able to reject samples from such that they are sampled from , must “cover” or envelop the distribution . This is generally done by choosing a constant such that   for all . For this reason is often called the envelope distribution. A common criterion for accepting samples from is based on the ratio of the target distribution to that of the envelope distribution. The samples are accepted if

where , and rejected otherwise. If the ratio is close to one, then must have a large amount of probability mass around and that sample should  be more likely accepted. If the ratio is small, then it means that has low probability mass around and we should be less likely to accept the sample. This criterion is demonstrated in the chunk of MATLAB code and the resulting figure below:

rand('seed',12345);
x = -10:.1:10;
% CREATE A "COMPLEX DISTRIBUTION" f(x) AS A MIXTURE OF TWO NORMAL
% DISTRIBUTIONS
f = inline('normpdf(x,3,2) + normpdf(x,-5,1)','x');
t = plot(x,f(x),'b','linewidth',2); hold on;

% PROPOSAL IS A CENTERED NORMAL DISTRIBUTION
q = inline('normpdf(x,0,4)','x');

% DETERMINE SCALING CONSTANT
c = max(f(x)./q(x))

%PLOT SCALED PROPOSAL/ENVELOP DISTRIBUTION
p = plot(x,c*q(x),'k--');

% DRAW A SAMPLE FROM q(x);
qx = normrnd(0,4);
fx = f(qx);

% PLOT THE RATIO OF f(q(x)) to cq(x)
a = plot([qx,qx],[0 fx],'g','Linewidth',2);
r = plot([qx,qx],[fx,c*q(qx)],'r','Linewidth',2);
legend([t,p,a,r],{'Target','Proposal','Accept','Reject'});
xlabel('x');

Rejection Sampling with a Normal proposal distribution

Here a zero-mean Normal distribution is used as the proposal distribution. This distribution is scaled by a factor , determined from and to ensure that the proposal distribution covers . We then sample from , and compare the proportion of occupied by . If we compare this proportion to a random number sampled  from (i.e. the criterion outlined above), then we would accept this sample with probability proportional to the length of the green line segment and reject the sample with probability proportional to the length of the red line segment.

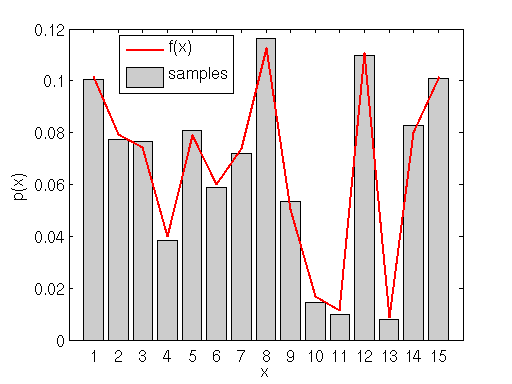
Rejection sampling of a random discrete distribution

This next example shows how rejection sampling can be used to sample from any arbitrary distribution, continuous or not, and with or without an analytic probability density function.

Random Discrete Target Distribution and Proposal that Bounds It.

The figure above shows a random discrete probability density function generated on the interval (0,15). We will use rejection sampling as described above to sample from . Our proposal/envelope distribution is the uniform discrete distribution on the same interval (i.e. any of the integers from 1-15 are equally probable) multiplied by a constant that is determined such that the maximum value of lies under (or equal to) .

Rejection Samples For Discrete Distribution on interval [1 15]

Plotted above is the target distribution (in red) along with the discrete samples obtained using the rejection sampling. The MATLAB code used to sample from the target distribution and display the plot above is here:

rand('seed',12345)
randn('seed',12345)

fLength = 15;
% CREATE A RANDOM DISTRIBUTION ON THE INTERVAL [1 fLength]
f = rand(1,fLength); f = f/sum(f);

figure; h = plot(f,'r','Linewidth',2);
hold on;
l = plot([1 fLength],[max(f) max(f)],'k','Linewidth',2);

legend([h,l],{'f(x)','q(x)'},'Location','Southwest');
xlim([0 fLength + 1])
xlabel('x');
ylabel('p(x)');
title('Target (f(x)) and Proposal (q(x)) Distributions');

% OUR PROPOSAL IS THE DISCRETE UNIFORM ON THE INTERVAL [1 fLength]
% SO OUR CONSTANT IS
c = max(f/(1/fLength));

nSamples = 10000;
i = 1;
while i < nSamples
   proposal = unidrnd(fLength);
   q = c*1/fLength; % ENVELOPE DISTRIBUTION
   if rand < f(proposal)/q
      samps(i) = proposal;
      i = i + 1;
   end
end

% DISPLAY THE SAMPLES AND COMPARE TO THE TARGET DISTRIBUTION
bins = 1:fLength;
counts = histc(samps,bins);
figure
b = bar(1:fLength,counts/sum(counts),'FaceColor',[.8 .8 .8])
hold on;
h = plot(f,'r','Linewidth',2)
legend([h,b],{'f(x)','samples'});
xlabel('x'); ylabel('p(x)');
xlim([0 fLength + 1]);

Rejection sampling from the unit circle to estimate

Though the ratio-based acceptance-rejection criterion introduced above is a common choice for drawing samples from complex distributions, it is not the only criterion we could use. For instance we could use a different set of criteria to generate some geometrically-bounded distribution. If we wanted to generate points uniformly within the unit circle (i.e. a circle centered at and with radius ), we could do so by sampling Cartesian spatial coordinates and uniformly from the interval (-1,1)–which samples form a square centered at (0,0)–and reject those points that lie outside of the radius

Unit Circle Inscribed in Square

Something clever that we can do with such a set of samples is to approximate the value : Because a square that inscribes the unit circle has area:

and the unit circle has the area:

We can use the ratio of their areas to approximate :

The figure below shows the rejection sampling process and the resulting estimate of from the samples. One-hundred thousand 2D points are sampled uniformly from the interval (-1,1).  Those points that lie within the unit circle are plotted as blue dots. Those points that lie outside of the unit circle are plotted as red x’s. If we take four times the ratio of the area in blue to the entire area, we get a very close approximation to 3.14 for .

Rejection Criterion

The MATLAB code used to generate the example figures is below:

% DISPLAY A CIRCLE INSCRIBED IN A SQUARE

figure;
a = 0:.01:2*pi;
x = cos(a); y = sin(a);
hold on
plot(x,y,'k','Linewidth',2)

t = text(0.5, 0.05,'r');
l = line([0 1],[0 0],'Linewidth',2);
axis equal
box on
xlim([-1 1])
ylim([-1 1])
title('Unit Circle Inscribed in a Square')

pause;
rand('seed',12345)
randn('seed',12345)
delete(l); delete(t);

% DRAW SAMPLES FROM PROPOSAL DISTRIBUTION
samples = 2*rand(2,100000) - 1;

% REJECTION
reject = sum(samples.^2) > 1;

% DISPLAY REJECTION CRITERION
scatter(samples(1,~reject),samples(2,~reject),'b.')
scatter(samples(1,reject),samples(2,reject),'rx')
hold off
xlim([-1 1])
ylim([-1 1])

piHat = mean(sum(samples.*samples)<1)*4;

title(['Estimate of \pi = ',num2str(piHat)]);

Wrapping Up

Rejection sampling is a simple way to generate samples from complex distributions. However, Rejection sampling also has a number of weaknesses:

• Finding a proposal distribution that can cover the support of the target distribution is a non-trivial task.
• Additionally, as the dimensionality of the target distribution increases, the proportion of points that are rejected also increases. This curse of dimensionality makes rejection sampling an inefficient technique for sampling multi-dimensional distributions, as the majority of the points proposed are not accepted as valid samples.
• Some of these problems are solved by changing the form of the proposal distribution to “hug” the target distribution as we gain knowledge of the target from observing accepted samples. Such a process is called Adaptive Rejection Sampling, which will be covered in another post.

Inverse Transform Sampling

There are a number of sampling methods used in machine learning, each of which has various strengths and/or weaknesses depending on the nature of the sampling task at hand. One simple method for generating samples from distributions with closed-form descriptions is Inverse Transform (IT) Sampling.

The idea behind IT Sampling is that the probability mass for a random variable distributed according to the probability density function  integrates to one and therefore the cumulative distribution function can be used to map from values in the interval (i.e. probabilities) to the domain of . Because it is easy to sample values uniformly from the interval , we can use the inverse of the CDF to transform these sampled probabilities into samples . The code below demonstrates this process at work in order to sample from a student’s t distribution with 10 degrees of freedom.

rand('seed',12345)

% DEGREES OF FREEDOM
dF = 10;
x = -3:.1:3;
Cx = cdf('t',x,dF)
z = rand;

% COMPARE VALUES OF
zIdx = min(find(Cx>z));

% DRAW SAMPLE
sample = x(zIdx);

% DISPLAY
figure; hold on
plot(x,Cx,'k','Linewidth',2);
plot([x(1),x(zIdx)],[Cx(zIdx),Cx(zIdx)],'r','LineWidth',2);
plot([x(zIdx),x(zIdx)],[Cx(zIdx),0],'b','LineWidth',2);
plot(x(zIdx),z,'ko','LineWidth',2);
text(x(1)+.1,z + .05,'z','Color','r')
text(x(zIdx)+.05,.05,'x_{sampled}','Color','b')
ylabel('C(x)')
xlabel('x')
hold off

IT Sampling from student’s-t(10)

However, the scheme used to create to plot above is inefficient in that one must compare current values of with the for all values of . A much more efficient method is to evaluate directly:

1. Derive (or a good approximation) from
2. for

• – draw from
• –
• – end for

The IT sampling process is demonstrated in the next chunk of code to sample from the Beta distribution, a distribution for which  is easy to approximate using Netwon’s method (which we let MATLAB do for us within the function icdf.m)

rand('seed',12345)
nSamples = 1000;

% BETA PARAMETERS
alpha = 2; beta = 10;

% DRAW PROPOSAL SAMPLES
z = rand(1,nSamples);

% EVALUATE PROPOSAL SAMPLES AT INVERSE CDF
samples = icdf('beta',z,alpha,beta);
bins = linspace(0,1,50);
counts = histc(samples,bins);
probSampled = counts/sum(counts)
probTheory = betapdf(bins,alpha,beta);

% DISPLAY
b = bar(bins,probSampled,'FaceColor',[.9 .9 .9]);
hold on;
t = plot(bins,probTheory/sum(probTheory),'r','LineWidth',2);
xlim([0 1])
xlabel('x')
ylabel('p(x)')
legend([t,b],{'Theory','IT Samples'})
hold off

Inverse Transform Sampling of Beta(2,10)

Wrapping Up

The IT sampling method is generally only used for univariate distributions where can be computed in closed form, or approximated. However, it is a nice example of how uniform random variables can be used to sample from much more complicated distributions.